Insights
The idea of characterizing the statistical variability of the traits of the human face dates back to the early ’80s. This idea was extended further in the work of Blanz and Vetter that proposed to construct a 3D morphable model (3DMM) from a set of example 3D face scans.
Similarly to the 2D case, the idea here is to capture the 3D face variability in the training data using an average model and a set of deformation component. The statistical model is then capable of generating new face instances with plausible shape and appearance.
In order to guarantee the 3DMM capability of generalizing to new unseen identities, the training set should include the necessary variability in terms of gender, age and ethnicity. Furthermore, including in the training set scans with facial expressions is also required to enable the 3DMM to generalize to expressive data.
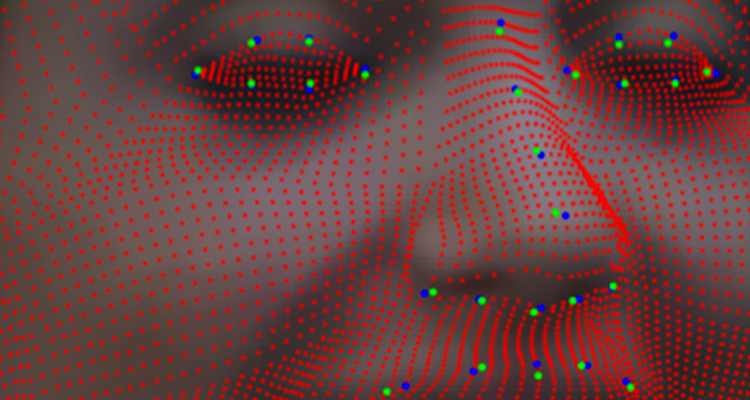
In order to derive a statistics of the face variability in the training data, a dense point-to-point correspondence between the vertices of the training scans should be established. This process can be seen as a sort of mesh reparametrization, where corresponding points in all the scans must have the same semantic meaning (for example, the vertex with index i must represent the left mouth corner in all the scans).
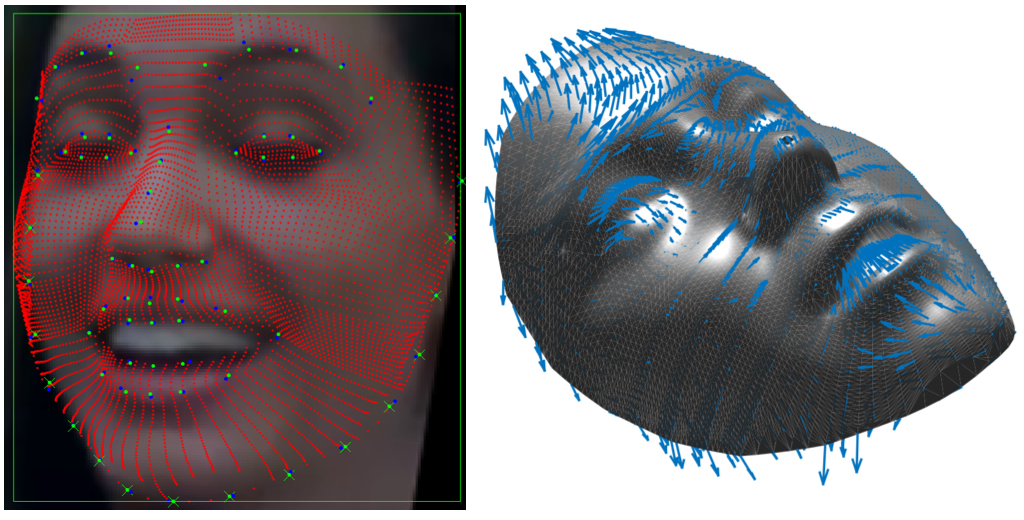
Once a dense correspondence is established across the training data, the statistical variability of every vertex of the scans can be modeled. Here we propose to learn a dictionary of deformation components; to do this, we first learn a basis (dictionary) from the training set, then we use linear combinations of such basis to deform the average model. In order to fit the 3DMM to a target face in a test image, we need firstly to get an estimate of the 3D pose of the face (rigid transformation), and then to deform the 3DMM to the image (non-rigid transformation).
Given a face framed in an image, its 3D pose can be estimated by establishing a correspondence between a set of facial landmarks detected both in 2D and 3D. Once this correspondence is established and the pose is obtained, the average model is deformed in order to minimize the difference between the 2D and projected 3D landmarks locations. The statistics of the faces extracted from the train set of 3D scans ensures that the deformations involve larger areas of the 3D model.
We then exploit the projection on the image of the 3DMM to sample RGB values in correspondence of the projected vertices, so as to render a frontal view. These latter images are then used to compute Local Binary Patterns (LBP) descriptors over patches centered on the projected vertices of the 3DMM instead of considering a regular grid over the image.
The latter approach for constructing a 3D morphable model proved to enhance the standard PCA based approach.