Insights
One of the most important tasks related to Computer Vision is visual object tracking. The task of multiple target tracking is to follow targets in an uncontrolled environment (Figure 1) while at the same time handling problems such as occlusion, similarity in the target appearance and crowded scenes.
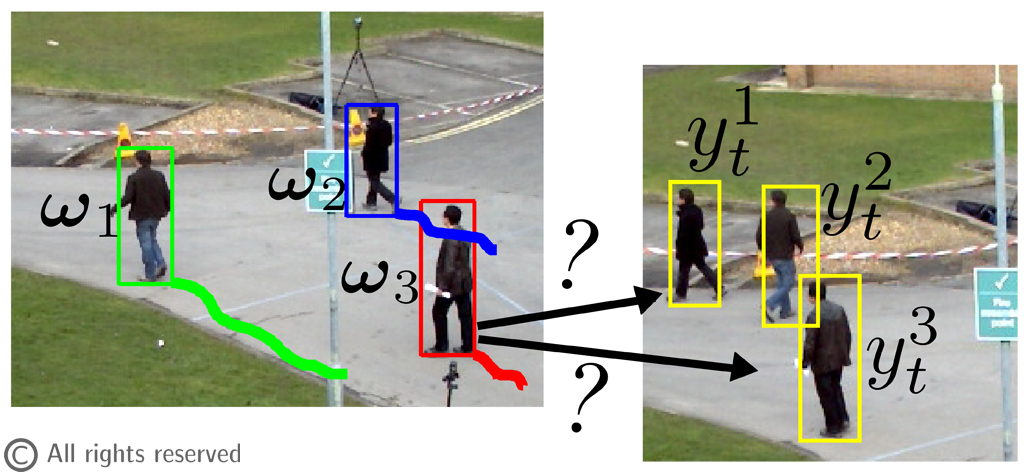
Figure 1: The data association problem. At each time instant observations y must be associated with one of the running trackers ⍵.
In this research project we present an an end-to-end multi-target tracking system that uses the machinery of sparse basis expansions. Starting from noisy detections in video sequences, our approach attempts to reconstruct new observations using a regularized linear combination of tracklets already identified. We create a discriminative basis B of observations (an example is shown in upper part of Figure 2) that we use to reconstruct and associate new targets in the data association phase. Data association is implemented via two different types of association phases: a local data association phase that looks at recent observations only, and a global association phase that looks at the entire sequence of associations up to a given time and enforces a long-term measure of association consistency. The use of regularized basis expansions allows our system to exploit multiple instances of the target when performing data association rather than relying on an average representation of target appearance. In addition the new global association phase allow to reduce the number of id switches and tracklet fragmentation.
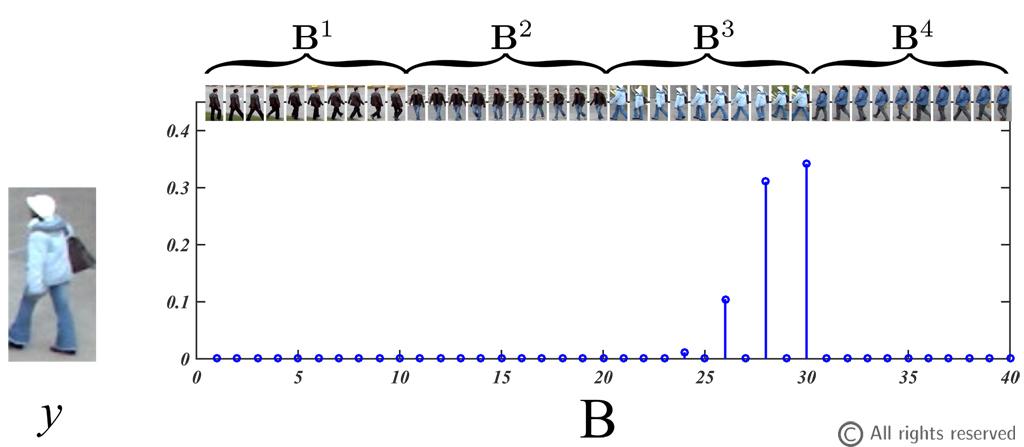
Figure 2: Sparse basis expansion. An observation y is reconstructed in terms of a basis of tracklet observations.
The data association (DA) problem is one of the main hurdles to be overcome in multiple target tracking and consists of finding the right assignment between the set of tracked targets and the set of new observations extracted from the current frame of a sequence. This task may become difficult in real-world scenarios due to many problems that may arise. One problem is how to create a representation that discriminatively models each target through time, while another is how to build an accurate rule for discerning each subject from the others in the scene. Moreover, if we consider real time constraints, data association must scale well with the number of targets.
The key idea behind our approach is the construction and use of a discriminative basis B (e.g. Figure 2) used in a regularized optimization problem to perform a sparse reconstruction of an unknown target. Our local data association phase only considers the current frame and current set of tracklets. It relies on the solution of a regularized basis expansion problem to determine the possible association of new detections to existing tracklets. We maintain a discriminative basis for each tracklet, composed of the features computed from all detections associated to the tracklet. The discriminative basis B is used to perform a sparse reconstruction of an unknown detection, obtaining reconstruction coefficients. More precisely, the coefficient strength (lower part in figure 2) indicates which basis vectors of a tracked target contribute most to the sparse reconstruction. These coefficients are used in our system to verify how much affinity there is between the new detection y and each tracklet k.
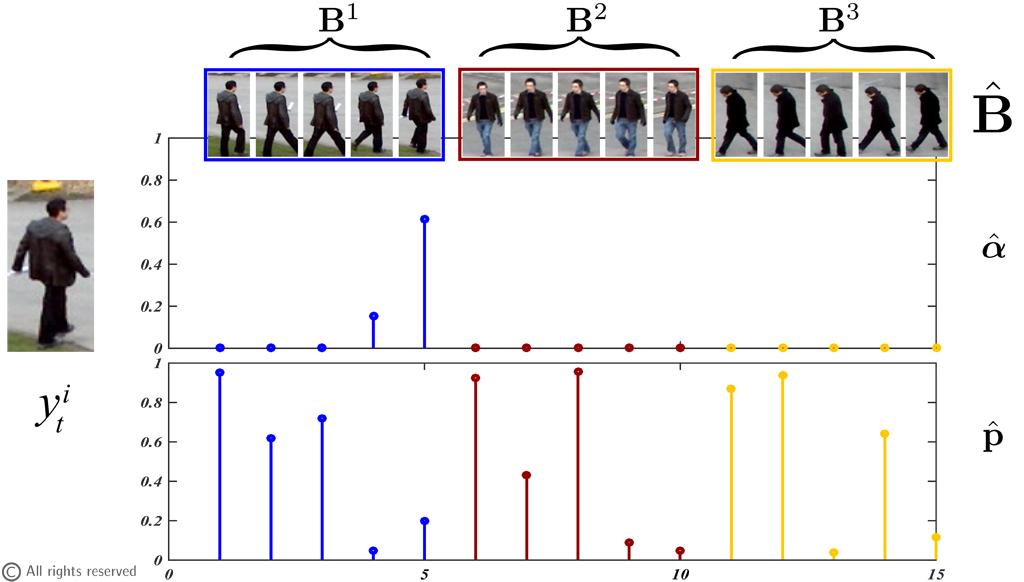
Figure 3: Sparse Weighted Reconstruction. Example of the sparse vector (the upper distribution) uses to reconstruct a new observation y obtained with the weighted sparse reconstruction. The weights vector (lower distribution) is used in the sparse reconstruction to compute the sparse vector.
During the multi-target tracking process multiple trajectories are created. It may happen that more than one corresponds to the same subject. This problem is referred to as tracklet fragmentation, and to resolve these types of problems, we define the global data association phase. Our approach estimates a compatibility score C between existing tracklets in a leave-one-out manner and merge them by a greedy pairing if this score is high. The computation of the compatibility scores is based on a weighted version of the regularized reconstruction already being used for local data association. To estimate the compatibility between existing tracklets we prioritize the templates of each sub-basis that are used most frequently during the tracking process and can thus be considered as more representative (e.g. Fig. 3). The proposed approach obtains good results comparable with the state-of-the-art on two benchmark datasets. Our ongoing research is focused on integrating global and local data association into a single, continuous framework that obviates the need to run global association at arbitrary intervals during the tracking process.
PUBLICATIONS:
- Andrew D. Bagdanov, Alberto Del Bimbo, Dario Di Fina, Svebor Karaman, Giuseppe Lisanti, Iacopo Masi, “Multi-target Data Association Using Sparse Reconstruction”. ICIAP (2) 2013: 239-248.
- Dario Di Fina, Giuseppe Lisanti, Svebor Karaman, Andrew D. Bagdanov and Alberto Del Bimbo, “Multi-Target Tracking using Weighted Sparse Reconstruction”, Submitted to Pattern Analysis and Applications, 2015.